在数学中,最速降曲线是指从一个点到另一个点的路径中,使得时间最短的曲线。而在工程学、物理学和经济学中,最速降曲线的应用非常广泛,如汽车行驶路径规划、物体运动轨迹预测等。本文将通过对最速降曲线的探究,解析其背后所隐藏的极值问题,并给出相关的数学方程式。
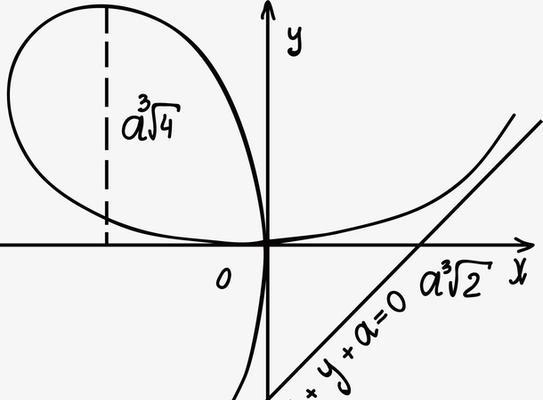
一:最速降曲线的定义及求解方法
最速降曲线的定义是指从点A到点B,沿一条曲线到达B点,其时间最短。其求解方法是要使该曲线在任意点的切线斜率等于某一常数k,那么该曲线即为最速降曲线。
二:极值问题的基础知识
极值问题是数学中常见的问题之一,涉及到函数的最大值和最小值。解决极值问题需要掌握导数概念和求导数的方法。
三:导数的概念及意义
导数是函数在某一点处的变化率,可表示为函数y=f(x)在x点处的斜率。导数的意义在于可以用来表示函数的最值和方向。
四:求解最速降曲线的一般方法
求解最速降曲线的一般方法是先确定初始点和终止点,然后列出满足条件的微分方程,再根据微分方程求解曲线方程。
五:利用拉格朗日乘数法求解最速降曲线
拉格朗日乘数法是一种常用的求解约束极值问题的方法,可以用来求解最速降曲线。具体方法是在满足微分方程的条件下,通过引入拉格朗日乘数来约束初始点和终止点。

六:最速降曲线问题与伯努利方程
伯努利方程是流体力学中的一个基本方程,可以用来描述流体在不同位置、不同速度下的压力和动能关系。最速降曲线问题与伯努利方程有密切的关系,可通过伯努利方程来求解最速降曲线问题。
七:最速降曲线问题的实际应用
最速降曲线问题在工程学、物理学和经济学中有着广泛的应用,如汽车行驶路径规划、物体运动轨迹预测等。通过最速降曲线可以优化路径规划,提高效率和节省时间成本。
八:最速降曲线问题与机器学习
最速降曲线问题在机器学习中也有着广泛的应用,如神经网络训练、回归分析等。机器学习通过最速降曲线问题来优化算法的学习过程,提高算法的准确性和鲁棒性。
九:最速降曲线问题的局限性
尽管最速降曲线问题具有广泛的应用场景,但它也存在一定的局限性。例如,最速降曲线只适用于起点和终点确定的情况,无法解决多起点或多终点的问题。
十:最速降曲线问题与路径规划
在路径规划中,最速降曲线问题是一个重要的研究方向。例如,智能驾驶中的车辆行驶路径规划问题就可以通过最速降曲线来优化行驶路径,提高行驶安全性和效率。
十一:最速降曲线问题与优化算法
最速降曲线问题在优化算法中也有着广泛的应用。例如,梯度下降算法就可以通过最速降曲线来优化目标函数,提高算法的收敛速度和准确性。
十二:最速降曲线问题的数学模型
最速降曲线问题可以用数学模型来表示。例如,在平面直角坐标系中,最速降曲线可表示为一条反比例函数,其斜率为常数k。
十三:最速降曲线问题的求解步骤
求解最速降曲线问题的步骤是先确定起点和终点,再列出微分方程,通过微分方程求解曲线方程,最后验证是否满足极值条件。
十四:最速降曲线问题的意义及价值
最速降曲线问题不仅具有理论意义,还具有实际应用价值。通过最速降曲线问题的研究,可以优化路径规划、提高算法性能、推动智能化发展等。
十五:
最速降曲线问题是数学中的一个重要研究方向,涉及到极值问题、微分方程、伯努利方程等多个领域。其应用价值非常广泛,可用于路径规划、算法优化、智能驾驶等多个领域。